Think-in-Systems
An intuitive Introduction to Systems Engineering and Dynamics
Project maintained by sohamphanseiitb Hosted on GitHub Pages — Theme by mattgraham
The Systems Zoo - One Stock Systems
Lets take the instance of the amount of money deposited in a bank account as our stock. Taking the annual rate of expenditure to be a% of the total amount of money and b% be the annual rate of interest. We try to model this simple 1 stock system with the help of preliminary differential equations and the models represented above. Let the initial amount deposited in the account be c.
Observe the figure carefully. The toal amount of interest earned on the savings depends on the ‘Rate of Interest’ and amount of money in the account. This leads to a reinforcing feedback loop, as to keeping interest rate constant, interest getting deposited back to the balance, creates more interest, which in turns increases the balance, giving rise to an exponential growth tendency (very similar to the compound interest model used in savings banks). On the other hand, the expenditure loop is a balancing loop i.e keeping the expenditure rate constant, the larger the available balance, larger the expenditure, lesser the remaining stock, lesser the expenditure. Hence as the balance increases the expenditure increases and the interest also increases. But increase in expenditure decreases the stock levels and decreases the expenditure in future. However an increase in interest increases the stock levels and increases the interest in future. You can see that just by reversing the flows into and out of the system how varied behaviors we can obtain. That is truly yhr beauty of systems. However Based on the above model we formulate the governing equation for the same. Let x(t) be the total amount of money in the account at time t (in years, t=0 corresponds to base year)
\(x(t) = x(t-1) + x(t-1)\times\frac{b-a}{100}\hspace{10pt} t>0\)
\(x(t) = x(0) \hspace{10pt} t=0\)
We propagate our model by calculating values. By considering different expenditure and interest rates for the same initial amount we can inspect the behaviour of the stock level.
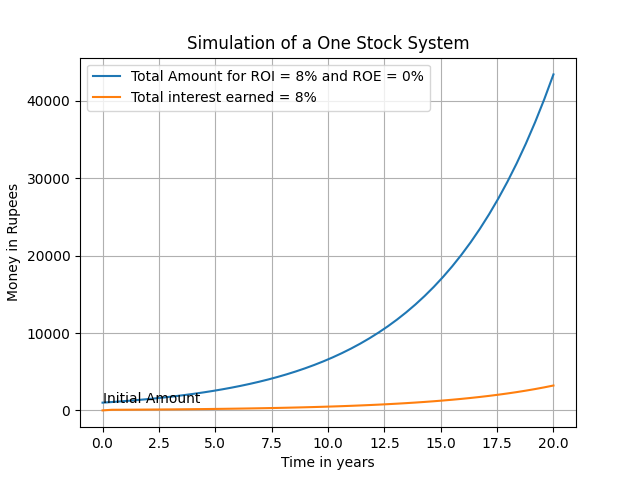
Based on the figure we can conclude that when the ROI (Rate of Interest) and ROE(Rate of Expenditure) are equal the stock level will be maintained at a constant rate. We explore the stock level behaviour when either of the ROI or ROE are zero. When we have a zero ROE and a finite ROI, we can see exponentialgrowth in the stock levels, thus we can conclude that in such an event it is the reinforcing loopthat regulates the behaviour of the stock level and causes such exponential growth. Whereasin the event of zero ROI but finite ROE, we can see that the decline is very slow as comparedto the earlier case, hinting that there is a balancing loop regulating the behaviour. In the firstcase, more amount creates more interest, which results into more amount – inducing a couplingand eventually exponential nature. In the second case, less amount means less expenditurewhich results into better retention of the available amount – displaying the balancing nature.
We have used the tools to simulate a system’s response in different conditions. Here, being a single stock system, it was easy to calculate and get the results. Systems get complicated when there are multiple stocks, feedbacks and external factors affecting stock level and flows.